A positivity-preserving scheme for fluctuating hydrodynamics

Capillary wave spectrum for a liquid slab in equilibrium with its vapour, obtained from the hybrid positivity-preserving scheme and a standard upwind scheme, compared with the theoretical prediction. The small inset shows one of the configurations of the system with the liquid slab at the center and two rough liquid-vapour interfaces.
Capillary wave spectrum for a liquid slab in equilibrium with its vapour, obtained from the hybrid positivity-preserving scheme and a standard upwind scheme, compared with the theoretical prediction. The small inset shows one of the configurations of the system with the liquid slab at the center and two rough liquid-vapour interfaces.

A natural constraint in the numerical study of physical and technological problems is the positivity of relevant quantities such as density, temperature and concentration. This is crucially important when the systems under consideration are subject to stochastic forcing in which case unphysical negative values of the relevant quantities result, eventually causing blow-up of the numerical solution. While “positivity-preserving” schemes are available for deterministic systems, little work has been done for stochastic ones, despite numerous applications where noise is crucial: from fluid-structure interaction to multiphase systems and bubble nucleation.

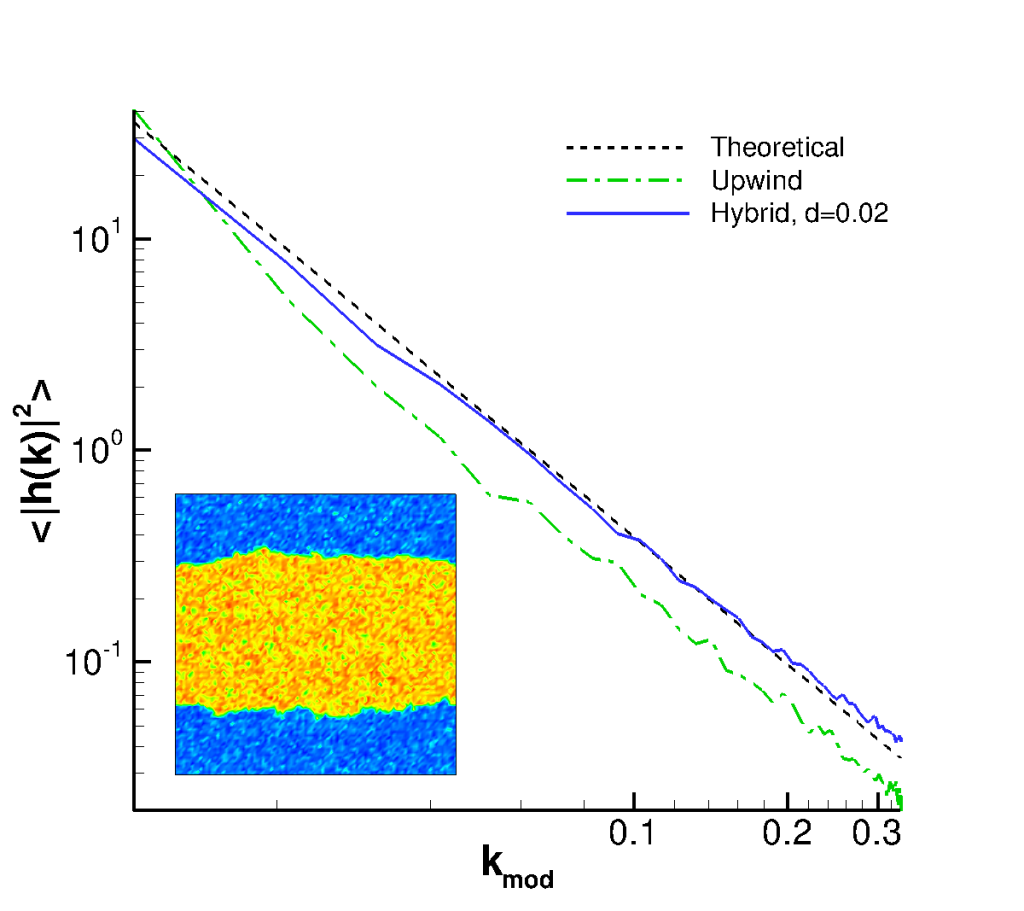
Here we formulate a positivity-preserving scheme for the isothermal equations of fluctuating hydrodynamics with both density and momentum being fluctuating fields. The scheme is a hybrid one combining upwind and central discretisations to take advantage of both the positivity-preserving property of the former and the (local) fluctuation-dissipation-balance compliance of the latter. The robustness of this hybrid approach is validated against several benchmark cases, including analytical predictions, both in single and two-phase systems.

Authors: Magaletti, Francesco; Gallo, Mirko; Perez, Sergio P.; Carrillo, Jose A.; Kalliadasis, Serafim

https://www.sciencedirect.com/science/article/pii/S0021999122003102