Physics-informed Bayesian inference of external potentials in classical density-functional theory

Data-Driven Solution of the Inverse Problem in Classical Statistical Mechanics

Statistical mechanics aims to relate observable macroscopic properties of matter with its underlying microscopic structure via appropriate averaging. The central property which facilitates such averaging is the probability density ρ(r) of finding a particle near position-vector r. Finding ρ(r) can therefore be viewed as the direct problem of statistical mechanics. One way to find ρ(r) is by minimising the free energy of the many-body system, expressed as a functional of ρ(r). Approaches based on this general idea are collectively known as Density Functional Theories (DFTs). Our work discusses DFTs of classical systems.

Usually DFT approximations are interpretable and amenable to computation. This explains the popularity of DFTs across fundamental applications of statistical mechanics. However therein lies the principal challenge of using DFTs in engineering: one must know (or postulate) the density functional of the system under consideration. This is highly challenging in realistic scenarios encountered in, e.g., biology, nanotechnology and chemical engineering. Our work aims to address this challenge.   

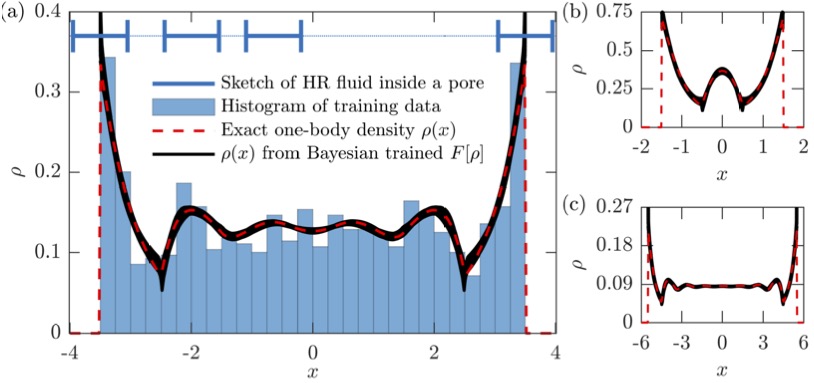
We pose the inverse problem of statistical mechanics: given particle data, characterise the free energy functional of the system. We then solve it using Bayesian reasoning. In the process, we develop a data-efficient learning algorithm that automates the construction of approximate free-energy functionals from small amounts of simulation data. On output the user gets a probability distribution over DFTs with full uncertainty quantification, allowing one to scale the description to system sizes far beyond the simulation capabilities. Our approach leverages modern computational capabilities in a physics-constrained framework to learn the free energy in a data-driven automated fashion. We validate our algorithm by consideing classical particle systems with excluded volume interactions. Such systems are ubiquitous in nature, while being highly challenging in terms of free energy modeling. We demonstrate that with appropriate particle data we can learn both the canonical and grand-canonical free-energy representations of such systems. Extensions to more complex and higher-dimensional systems are conceptually straightforward.

Authors: Antonio Malpica-Morales, Peter Yatsyshin, Miguel A.Duran-Olivencia, Serafim Kalliadasis

Journal of Chemical Physics, Volume 159, Issue 10, DOI 10.1063/5.0146920