Weyl nodes in Ce3Bi4Pd3 revealed by dynamical mean-field theory

In the quantum theory of solids, (non-interacting) electrons are described by (one-particle) wave-functions and their binding energies assume discrete (quantised) values. In the last few decades, it has been realized that there are particular settings in which these wave-functions and energies have characteristics (linked to the mathematical field of topology) that, while seemingly inconspicuous at first glance, can lead to spectacular properties. Examples include the quantum (anomalous) Hall effect, or, more generally, the presence of metal-like states on the surface of particular insulators. More recent is the study of topological effects in systems in which electrons interact strongly with each other.

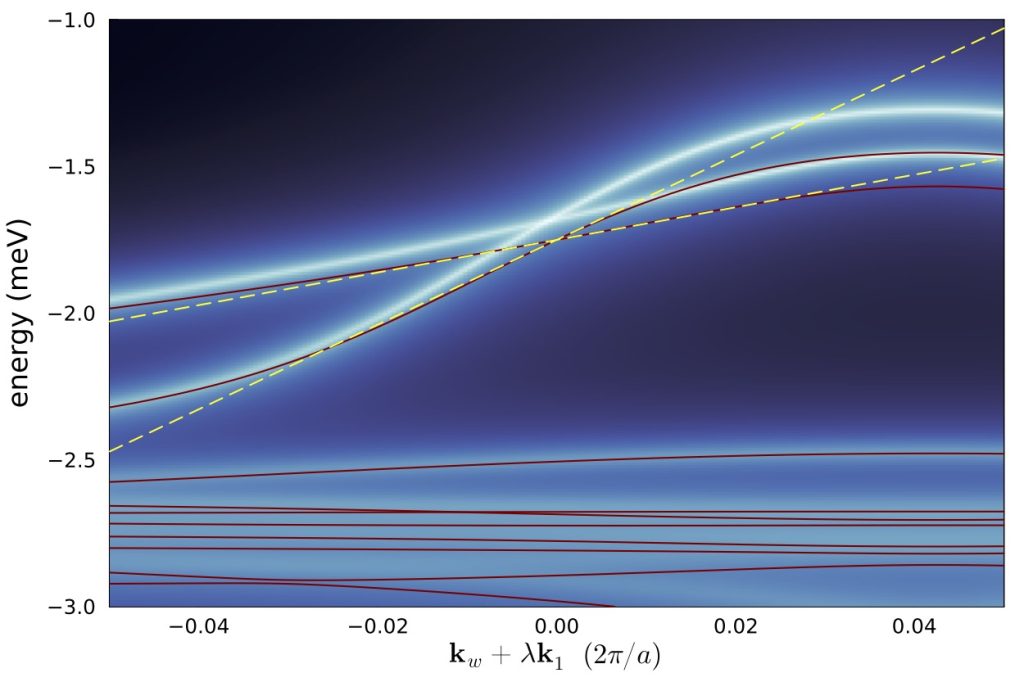
In the current work, Braß et al investigate a potential source for the intriguing spontaneous Hall effect measured in the strongly correlated semi-metal Ce3Bi4Pd3. Using dynamical mean-field theory (DMFT), we construct a strongly renormalized quasi-particle (QP) Hamiltonian. Analysing its topological structure, we evidence that many-body effects lead to the emergence of so-called Weyl-nodes. These are points of energy degeneracy that carry a topological charge — see the crossing point in the energy-vs-momentum curves in the figure; eigenvalues of the QP-Hamiltonian (red lines) on top of the DMFT spectral function (colour map). Indeed, we find that for decreasing temperature, the Kondo effect in this system leads to quasi-particle coherence and propels the Weyl-points towards the Fermi surface, where they will strongly influence transport properties. 

Authors: Martin Braß, Jan M. Tomczak, and Karsten Held

DOI: https://doi.org/10.1103/PhysRevResearch.6.033227